토목기사 필기 빈출문제(응용역학)-2
1. 단면 2차 모멘트가 I이고 길이가 L인 균일한 단면의 직선상(直線狀)의 기둥이 있다. 지지상태가 일단 고정, 타단 자유인 경우 오일러(Euler) 좌굴하중(Pcr)은? (단, 이 기둥의 영(Young)계수는 E이다.)

해설

※ 다른 경우들
양단 고정: 양쪽 끝이 모두 고정되어 있는 경우, 기둥은 좀 더 안정적이고, 유효 길이는 실제 길이의 반으로 간주됩니다.

한쪽 고정, 한쪽 힌지 (고정-힌지): 한쪽 끝이 고정되고 다른 쪽 끝이 힌지로 연결되어 있는 경우, 유효 길이는 실제 길이의 root(2) 배로 간주됩니다.

2. 그림과 같은 모멘트 하중을 받는 단순보에서 B지점의 전단력은?

①-1.0 kN ② -10 kN
③ -5.0 kN ④ -50 kN
해설
수직 방향의 평형 (수직 반력의 합 = 0, 왜냐하면 수직 방향의 외력이 없기 때문에)

모멘트의 평형: A 지점에 대한 모멘트 평형을 취하면, B 지점에서의 반력이 생성하는 모멘트와 B 지점에 작용하는 반시계 방향 모멘트의 합은 A 지점에 작용하는 시계 방향 모멘트와 같아야 합니다.

B 지점에 대한 모멘트 평형을 취하면, A 지점에서의 반력이 생성하는 모멘트와 A 지점에 작용하는 시계 방향 모멘트의 합은 B 지점에 작용하는 반시계 방향 모멘트와 같아야 합니다:

3. 그림과 같은 단순보에서 휨모멘트에 의한 탄성변형에너지는? (단, EI는 일정하다.)

해설
단순보에 등분포하중 (단위는 kN/m 또는 )이 작용할 때, 휨모멘트에 의한 탄성변형에너지는 다음 공식을 사용하여 계산할 수 있습니다:


그냥 외우는게 좋습니다.
4. 그림과 같은 직사각형 보에서 중립축에 대한 단면계수 값은?
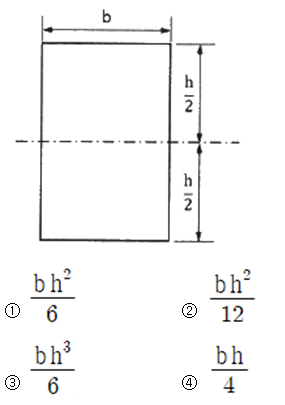
해설
※ 단면계수
단면의 저항 능력을 나타내는 값으로, 휨 응력을 계산할 때 사용
단면 이차 모멘트를 단면의 가장 끝단에서 도심(centroid)까지의 거리로 나눈 값
직사각형 단면의 경우, 중립축은 높이의 중앙, 즉 ℎ에 위치합니다.

5. 그림과 같은 부정정보에서 B점의 반력은?(암기)
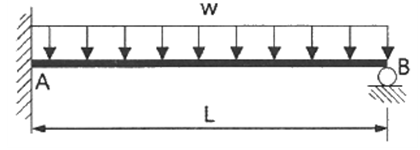
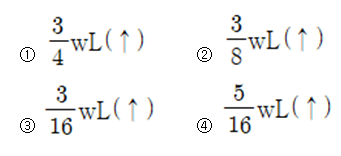
해설
무작정 외울수도 있지만, 처짐공식을 활용하면된다1) 캔틸레버보에 등분포 하중시 B점의 처짐
2) 캔틸레버보에 집중하중 시 B점의 처짐
1) - 2) = 0이면 되는데
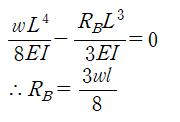
암기하자
'기사 > 토목기사 건축기사' 카테고리의 다른 글
| 토목기사 필기 빈출문제(토질역학)-2 (0) | 2024.04.17 |
|---|---|
| 토목기사 필기 빈출문제(수리수문학)-2 (0) | 2024.04.15 |
| 토목기사 필기 빈출문제(철근콘크리트)-1 (0) | 2024.04.01 |
| 토목기사 필기 빈출문제(토질역학)-1 (0) | 2024.03.28 |
| 토목기사 필기 빈출문제(수리수문)-1 (0) | 2024.03.26 |








