토목기사 필기 빈출문제(응용역학)-1
기사/토목기사 건축기사2024. 3. 25. 23:12
728x90
<응용역학>
1. 다음 그림과 같은 보에서 B 지점의 반력이 2P가 되기 위한 b/a는?

① 0.75 ② 1.00
③ 1.25 ④ 1.50
해설
R(반력) = Ra + Rb = P
Rb = 2P, Ra = -P
M(b) = Pa - Pb = 0
a = b
b/a = 1
2. 탄성계수(E)가 2.1×10^5MPa, 푸아송 비(ν)가 0.25일 때 전단탄성계수(G)의 값은?
① 8.4×10^4MPa ② 9.8×10^4MPa
③ 1.7×10^6MPa ④ 2.1×10^6MPa
해설


3. 길이 5m의 철근을 200MPa의 인장응력으로 인장하였더니 그 길이가 5mm만큼 늘어났다고 한다. 이 철근의 탄성계수는? (단, 철근의 지름은 20mm이다.)
① 2×10^4MPa ② 2×10^5MPa
③ 6.37×10^4MPa ④ 6.37×10^5MPa
해설

4. 양단고정의 장주에 중심축하중이 작용할 때 이 기둥의 좌굴응력은? (단, E=2.1×10^5MPa이고, 기둥은 지름이 4cm인 원형기둥이다.)

① 3.35MPa ② 6.72MPa
③ 12.95MPa ④ 25.91MPa
해설

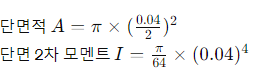

5. 다음 중 정(+)의 값뿐만 아니라 부(-)의 값도 갖는 것은?
① 단면계수 ② 단면 2차 반지름
③ 단면 2차 모멘트 ④ 단면 상승 모멘트
해설
단면 상승 모멘트는 단면의 끝 부분이 올라가거나 내려가는 경우에 발생하는 모멘트이므로, 양수 또는 음수 값이 될 수 있습니다. 이와 달리, 단면계수, 단면, 단면 2차 반지름, 그리고 단면 2차 모멘트는 보통 양수 값만을 갖습니다.
- 단면계수 (Z): 단면의 휨 강성을 나타내는 값이며, 단면 2차 모멘트와 도심 거리의 비율로 계산됩니다. 항상 양수입니다.
- 식: Z = I / y
- I: 단면 2차 모멘트
- y: 도심 거리
- 단면 2차 반지름 (r): 단면 2차 모멘트를 단면 면적으로 나눈 값이며, 단면의 형상을 나타내는 값입니다. 항상 양수입니다.
- 식: r = root(I / A)
- A: 단면 면적
- 단면 2차 모멘트 (I): 단면이 축에 대해 회전하는 힘에 대한 저항력을 나타내는 값이며, 단면의 형상과 크기에 따라 결정됩니다. 양수 또는 음수 값을 가질 수 있습니다.
- 식: I = ∫y^2 dA
- dA: 단면 면적의 미소 단위
- 단면 상승 모멘트 (Q): 단면의 중심축을 기준으로 단면의 면적을 y축 방향으로 이동시켰을 때 발생하는 모멘트입니다. 양수 또는 음수 값을 가질 수 있습니다.
- 식: Q = ∫yA dA
- A: 단면 면적
728x90
'기사 > 토목기사 건축기사' 카테고리의 다른 글
| 토목기사 필기 빈출문제(토질역학)-1 (0) | 2024.03.28 |
|---|---|
| 토목기사 필기 빈출문제(수리수문)-1 (0) | 2024.03.26 |
| 토목기사 토질역학 필수공식(2/2) (1) | 2024.03.22 |
| 토목기사 토질역학 필수공식(1/2) (0) | 2024.03.20 |
| [토질역학] 액상화 방지 공법 (0) | 2024.02.28 |
댓글()








